2019 / 06 / 22

SmallPT —— 99 行代码光线追踪解析

光线追踪（Ray tracing）是三维计算机图形学中的特殊渲染算法：根据光路可逆原理，对每一个像素，沿着入射光线逆向追踪若干次反射、折射，进而计算此光线的颜色，把场景渲染出来。

理论上，光线追踪算法可以完整地模拟物理世界中的光照，分毫不差地计算出每个像素的颜色，但是这样做的算力消耗趋近于正无穷。所以实际上所有光线追踪算法都包含了一些近似优化的逻辑，以将运算开销控制在可接受的数量级内。

Rhythm & Hues Studios 公司的程序员 Kevin Beason 曾于 2010 年编写过一个名为 SmallPT 的 C++ 程序，仅包含 99 行代码，即实现了最简单的光线追踪效果。此程序可视为光追算法的可运行最小集，是初学者学习和理解光追原理的极佳材料，其运行结果如下图所示。作为一个门外汉，我花了好几个晚上研究这 99 行代码，并在这个极好的 PPT 的帮助下，总算基本弄明白了其运行的原理。不妨记录下来：

渲染方程

还是从最基础的渲染方程开始：

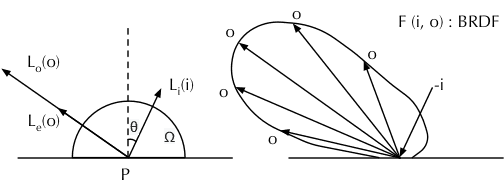
解释：

此方程描述的问题是：从物体表面上的一点处，射入到观察者眼中的某条光线的强度，是如何确定的。
为射入观察者眼中的光线的颜色，即需要求取的值；为出射方向。
为物体表面在点向观察者方向自发射的光线的颜色（灯）。
表示环境入射到点的光的颜色；代表入射方向（为计算方便，取真实入射方向的反方向，不影响代表关系，后面也简称为入射方向）。
表示在给定和时，由方向的入射单位光强产生的方向的出射光的强度，此函数与表面的性质有关，又称表面的 BRDF 函数。
表示与表面法线的夹角。
整个积分项表示：对半球（不透明材质）或全球（透明介质）内的所有入射方向进行积分，得到的方向的出射光强度。

依照光线追踪的原理，我们沿着方向追踪到一处交点，就需要进行一次积分操作。在计算机程序中，积分是用求和模拟的，求和的次数越多（自变量的间隔越小），结果就越准确。假设每次积分都要进行次求和操作，那么当追踪的光线遇到第一个交点时，会发散成条光线；同时追踪这条光线，到下一个交点，每条光线又会发散成条光线……随着追踪深度的增加，计算开销的量级将按照指数级上升。

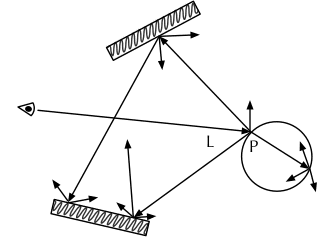
蒙特卡洛方法

蒙特卡洛方法（Monte Carlo method）是一种使用概率理论（通过大量随机数采样）进行数值计算以求取积分的方法。一个常用的有助理解的例子是：对「如何计算圆的面积」这个问题（圆的面积公式求取其实也是一个积分问题），蒙特卡洛的解法是「撒豆」：在包含圆的已知面积为的矩形内随机采样（撒豆）次，统计豆在圆内的次数为，则圆的面积为。

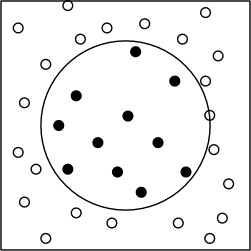
撒豆问题不仅可以解圆的面积，还可以解任意形状，甚至不规则形状的面积求取。

更具体地，蒙特卡洛方法可以表述为：

左侧表示函数在区间的积分，即下图中的部分阴影部分面积。
此积分的值，可以这样求取：随机在区间取值，采样计算，然后计算所有样本的均值并乘以区间的长度。当取样数量越大，最后的值就越接近真实的积分值。

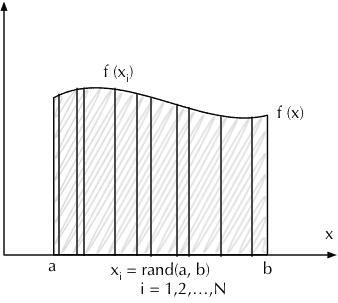
有同学可能会问（我也曾有此困惑），为什么不直接均等分采样，而要随机采样呢？其实，对于计算一维的函数，区别确实不大，但对二维甚至更高维度的函数（此时需要求取重积分）如，情况就不一样了。

此时，如果采取均等分采样，就需要选择在上均等分为若干份，选择在上均等分为若干份（其实撒豆问题已经是二维积分了，只不过积分函数是最简单的二值函数）。随着维度的增加，我们采样的数量也更难以控制，甚至还会出现维度不确定的情况。相比之下，蒙特卡洛方法的随机采样，可以轻易地控制或调整采样的次数：取两次（或更多次数的）随机数，可以视为单次随机行为，其背后包含的某种「随机性」是一致的。

对于光线追踪而言，我们会追踪若干次反射或折射（这个次数又称深度），每一次反射或折射都需要进行一次采样，相当于增加了一个维度。如果每次采样的次数过多，随着深度的增加，总采样次数很快就会不可接受，而如果每次的采样次数过少，（直觉告诉我）那么第一次采样对后续的采样将造成比较大的偏差（这背后应该有更完整的数学解释）。而且，在光线追踪算法中，有时候是否继续进行采样取决于具体的采样值，这就让等分采样变得更加困难。实际上，这份光追算法的实现，在每次反射或折射时只取一个随机样本，而通过增加总总采样次数来保证最后的结果满足期望。

光线追踪算法

使用蒙特卡洛方法，对每一次反射或折射不再进行积分，而是随机选取一条可能的反射或折射光线进行追踪。然后在开始追踪的源头处，重复多次追踪操作以求取期望，这就是 SmallPT 光追的算法。简述一下具体步骤：

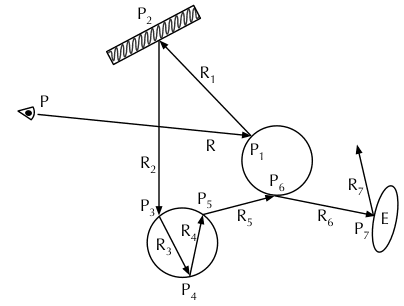
从每个像素处发出一条射线，其方向与入射到相机并产生该像素的光线相反。
求取此射线照射到的物体表面的点，即与场景中物体的交点；如有多个交点，取距离相机最近的那个。如果未求到交点，则返回背景色。
射向的光线强度，为本身发射光强度，加上反射或折射环境光的强度。
1. ：如果处是光源，则为光源的强度；否则，为 0。
2. ：根据处根据表面性质，按概率随机取一次反射的射线，然后重复 2 的步骤，分别递归地求取，，， ……等等，直到满足一些特定条件停止递归。

以上便是单个像素的光追的算法。对单个像素，重复大量的次数求取平均值，作为此像素的颜色。

对每个像素完成以上步骤，就渲染出了整幅图像。

代码摘录

完整的代码摘抄如下：

#include <math.h>   // smallpt, a Path Tracer by Kevin Beason, 2008
#include <stdlib.h> // Make : g++ -O3 -fopenmp smallpt.cpp -o smallpt
#include <stdio.h>  //        Remove "-fopenmp" for g++ version < 4.2
struct Vec {        // Usage: time ./smallpt 5000 && xv image.ppm
  double x, y, z;                  // position, also color (r,g,b)
  Vec(double x_=0, double y_=0, double z_=0){ x=x_; y=y_; z=z_; }
  Vec operator+(const Vec &b) const { return Vec(x+b.x,y+b.y,z+b.z); }
  Vec operator-(const Vec &b) const { return Vec(x-b.x,y-b.y,z-b.z); }
  Vec operator*(double b) const { return Vec(x*b,y*b,z*b); }
  Vec mult(const Vec &b) const { return Vec(x*b.x,y*b.y,z*b.z); }
  Vec& norm(){ return *this = *this * (1/sqrt(x*x+y*y+z*z)); }
  double dot(const Vec &b) const { return x*b.x+y*b.y+z*b.z; } // cross:
  Vec operator%(Vec&b){return Vec(y*b.z-z*b.y,z*b.x-x*b.z,x*b.y-y*b.x);}
};
struct Ray { Vec o, d; Ray(Vec o_, Vec d_) : o(o_), d(d_) {} };
enum Refl_t { DIFF, SPEC, REFR };  // material types, used in radiance()
struct Sphere {
  double rad;       // radius
  Vec p, e, c;      // position, emission, color
  Refl_t refl;      // reflection type (DIFFuse, SPECular, REFRactive)
  Sphere(double rad_, Vec p_, Vec e_, Vec c_, Refl_t refl_):
  rad(rad_), p(p_), e(e_), c(c_), refl(refl_) {}
  double intersect(const Ray &r) const { // returns distance, 0 if nohit
    Vec op = p-r.o; // Solve t^2*d.d + 2*t*(o-p).d + (o-p).(o-p)-R^2 = 0
    double t, eps=1e-4, b=op.dot(r.d), det=b*b-op.dot(op)+rad*rad;
    if (det<0) return 0; else det=sqrt(det);
      return (t=b-det)>eps ? t : ((t=b+det)>eps ? t : 0);
  }
};
Sphere spheres[] = {//Scene: radius, position, emission, color, material
  Sphere(1e5, Vec( 1e5+1,40.8,81.6), Vec(),Vec(.75,.25,.25),DIFF),//Left
  Sphere(1e5, Vec(-1e5+99,40.8,81.6),Vec(),Vec(.25,.25,.75),DIFF),//Rght
  Sphere(1e5, Vec(50,40.8, 1e5),     Vec(),Vec(.75,.75,.75),DIFF),//Back
  Sphere(1e5, Vec(50,40.8,-1e5+170), Vec(),Vec(),           DIFF),//Frnt
  Sphere(1e5, Vec(50, 1e5, 81.6),    Vec(),Vec(.75,.75,.75),DIFF),//Botm
  Sphere(1e5, Vec(50,-1e5+81.6,81.6),Vec(),Vec(.75,.75,.75),DIFF),//Top
  Sphere(16.5,Vec(27,16.5,47),       Vec(),Vec(1,1,1)*.999, SPEC),//Mirr
  Sphere(16.5,Vec(73,16.5,78),       Vec(),Vec(1,1,1)*.999, REFR),//Glas
  Sphere(600, Vec(50,681.6-.27,81.6),Vec(12,12,12),  Vec(), DIFF) //Lite
};
inline double clamp(double x){ return x<0 ? 0 : x>1 ? 1 : x; }
inline int toInt(double x){ return int(pow(clamp(x),1/2.2)*255+.5); }
inline bool intersect(const Ray &r, double &t, int &id){
  double n=sizeof(spheres)/sizeof(Sphere), d, inf=t=1e20;
  for(int i=int(n);i--;) if((d=spheres[i].intersect(r))&&d<t){t=d;id=i;}
  return t<inf;
}
Vec radiance(const Ray &r, int depth, unsigned short *Xi){
  double t;                               // distance to intersection
  int id=0;                               // id of intersected object
  if (!intersect(r, t, id)) return Vec(); // if miss, return black
  const Sphere &obj = spheres[id];        // the hit object
  Vec x=r.o+r.d*t, n=(x-obj.p).norm(), nl=n.dot(r.d)<0?n:n*-1, f=obj.c;
  double p = f.x>f.y && f.x>f.z ? f.x : f.y>f.z ? f.y : f.z; // max refl
  if (++depth>5) if (erand48(Xi)<p) f=f*(1/p); else return obj.e; //R.R.
  if (obj.refl == DIFF){                  // Ideal DIFFUSE reflection
    double r1=2*M_PI*erand48(Xi), r2=erand48(Xi), r2s=sqrt(r2);
    Vec w=nl, u=((fabs(w.x)>.1?Vec(0,1):Vec(1))%w).norm(), v=w%u;
    Vec d = (u*cos(r1)*r2s + v*sin(r1)*r2s + w*sqrt(1-r2)).norm();
    return obj.e + f.mult(radiance(Ray(x,d),depth,Xi));
  } else if (obj.refl == SPEC)            // Ideal SPECULAR reflection
    return obj.e + f.mult(radiance(Ray(x,r.d-n*2*n.dot(r.d)),depth,Xi));
  Ray reflRay(x, r.d-n*2*n.dot(r.d));     // Ideal dielectric REFRACTION
  bool into = n.dot(nl)>0;                // Ray from outside going in?
  double nc=1, nt=1.5, nnt=into?nc/nt:nt/nc, ddn=r.d.dot(nl), cos2t;
  if ((cos2t=1-nnt*nnt*(1-ddn*ddn))<0)    // Total internal reflection
    return obj.e + f.mult(radiance(reflRay,depth,Xi));
  Vec tdir = (r.d*nnt - n*((into?1:-1)*(ddn*nnt+sqrt(cos2t)))).norm();
  double a=nt-nc, b=nt+nc, R0=a*a/(b*b), c = 1-(into?-ddn:tdir.dot(n));
  double Re=R0+(1-R0)*c*c*c*c*c,Tr=1-Re,P=.25+.5*Re,RP=Re/P,TP=Tr/(1-P);
  return obj.e + f.mult(depth>2 ? (erand48(Xi)<P ? // Russian roulette
    radiance(reflRay,depth,Xi)*RP:radiance(Ray(x,tdir),depth,Xi)*TP) :
    radiance(reflRay,depth,Xi)*Re+radiance(Ray(x,tdir),depth,Xi)*Tr);
}
int main(int argc, char *argv[]){
  int w=1024/8, h=768/8, samps = argc==2 ? atoi(argv[1])/4 : 30;
  Ray cam(Vec(50,52,295.6), Vec(0,-0.042612,-1).norm()); // cam pos, dir
  Vec cx=Vec(w*.5135/h), cy=(cx%cam.d).norm()*.5135, r, *c=new Vec[w*h];
  for (int y=0; y<h; y++){                       // Loop over image rows
    fprintf(stderr,"\rRendering (%d spp) %5.2f%%",samps*4,100.*y/(h-1));
    for (unsigned short x=0, Xi[3]={0,0,(unsigned short)(y*y*y)}; x<w; x++)
      for (int sy=0, i=(h-y-1)*w+x; sy<2; sy++)     // 2x2 subpixel rows
        for (int sx=0; sx<2; sx++, r=Vec()){        // 2x2 subpixel cols
          for (int s=0; s<samps; s++){
            double r1=2*erand48(Xi), dx=r1<1 ? sqrt(r1)-1: 1-sqrt(2-r1);
            double r2=2*erand48(Xi), dy=r2<1 ? sqrt(r2)-1: 1-sqrt(2-r2);
            Vec d = cx*( ( (sx+.5 + dx)/2 + x)/w - .5) +
            cy*( ( (sy+.5 + dy)/2 + y)/h - .5) + cam.d;
            r = r + radiance(Ray(cam.o+d*140,d.norm()),0,Xi)*(1./samps);
          } // Camera rays are pushed ^^^^^ forward to start in interior
          c[i] = c[i] + Vec(clamp(r.x),clamp(r.y),clamp(r.z))*.25;
        }
  }
  FILE *f = fopen("image.ppm", "w");         // Write image to PPM file.
  fprintf(f, "P3\n%d %d\n%d\n", w, h, 255);
  for (int i=0; i<w*h; i++)
    fprintf(f,"%d %d %d ", toInt(c[i].x), toInt(c[i].y), toInt(c[i].z));
}

本文的主要部分，就是对这段代码的解析：

矢量运算

定义 Vec 结构体描述三维矢量，重载运算符来实现矢量运算。

struct Vec {
  double x, y, z;
  Vec(double x_=0, double y_=0, double z_=0){ x=x_; y=y_; z=z_; }
  Vec operator+(const Vec &b) const { return Vec(x+b.x,y+b.y,z+b.z); }
  Vec operator-(const Vec &b) const { return Vec(x-b.x,y-b.y,z-b.z); }
  Vec operator*(double b) const { return Vec(x*b,y*b,z*b); }
  Vec mult(const Vec &b) const { return Vec(x*b.x,y*b.y,z*b.z); }
  Vec& norm(){ return *this = *this * (1/sqrt(x*x+y*y+z*z)); }
  double dot(const Vec &b) const { return x*b.x+y*b.y+z*b.z; }
  Vec operator%(Vec&b){return Vec(y*b.z-z*b.y,z*b.x-x*b.z,x*b.y-y*b.x);}
};

矢量运算包括（假设；）：

加法 operator+：。
减法 operator-：。
乘法 mult()：。这种矢量分量直接相乘的运算通常用于颜色的计算，在三维空间中并无特殊的物理意义。
点乘 dot()：，其中为与的夹角。点乘的结果是一个标量，物理含义是在方向上的投影。
叉乘 operator%：，叉乘的结果是一个矢量，物理意义是垂直于和的矢量（按顺序右手螺旋），其长度为和构成的平行四边形面积。
矢量乘以标量 operator*：。
归一化 norm()：，其物理意义是保持矢量方向不变，将其长度缩放为单位长度 1。

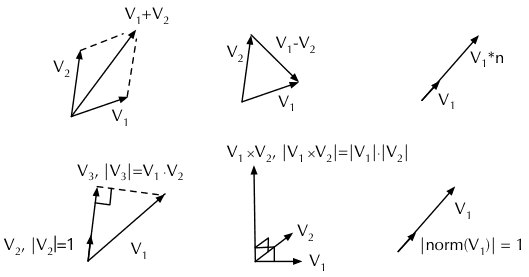
射线

通过定义射线的出射点和出射方向来定义射线：

struct Ray { Vec o, d; Ray(Vec o_, Vec d_) : o(o_), d(d_) {} };

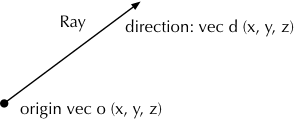
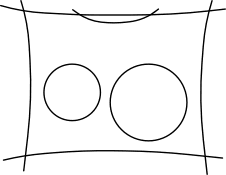
定义场景

如前文 SmallPT 的渲染效果图所示，整个场景由一个房间，一个光源和两个球体组成。为了简单，SmallPT 将场景全部用球体来表示，房间的墙壁就用直径极大（使观者感受不到墙壁是弯曲的）的球体来表示。

球体对象的表示

首先枚举出三种表面特性：散射面——用于墙壁，镜面——用于左侧的镜面小球，折射面——用于右侧的玻璃小球。
定义球体，内容包括：
1. 数值类型成员：半径；
2. 矢量类型成员：圆心位置，表面发光强度（颜色），表面散射颜色；
3. 表面特性；

enum Refl_t { DIFF, SPEC, REFR };  // material types, used in radiance()
struct Sphere {
  double rad;       // radius
  Vec p, e, c;      // position, emission, color
  Refl_t refl;      // reflection type (DIFFuse, SPECular, REFRactive)
  Sphere(double rad_, Vec p_, Vec e_, Vec c_, Refl_t refl_):
  rad(rad_), p(p_), e(e_), c(c_), refl(refl_) {}
  // ...
};

射线与球体相交

Sphere 上定义了 intersect 方法，以求取给定的射线与球体是不是相交。如果相交则返回射线原点与交点的距离。

double intersect(const Ray &r) const { // returns distance, 0 if nohit
  Vec op = p-r.o; // Solve t^2*d.d + 2*t*(o-p).d + (o-p).(o-p)-R^2 = 0
  double t, eps=1e-4, b=op.dot(r.d), det=b*b-op.dot(op)+rad*rad;
  if (det<0) return 0; else det=sqrt(det);
    return (t=b-det)>eps ? t : ((t=b+det)>eps ? t : 0);
}

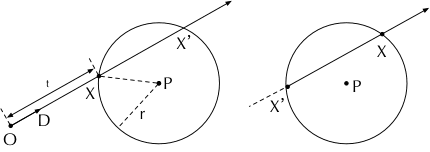
注意，下面为了清楚，我们使用大写字母为矢量，小写字母为标量来进行推导。我们需要求解的是射线的原点与交点的距离，而条件是：

点在射线上，即。
点在球面上，即与球心的距离等于球的半径。即，也就是。

将 (1) 中关于的表达式代入 (2)，得到：

展开得到：

这已经是一个一元二次方程，自变量是未知的。所有矢量经过平方或点积后都成为了标量，可以直接根据一元二次方程的求根公式：

计算出根。

一元二次方程可能没有实根的，此时射线与球体不相交。这对应着代码中 det<0 的情况，直接返回 0。
一元二次方程可能有两个实根，此时射线（所在的直线）与球体有两个交点。我们需要取的是最小的正根。如果另一个根（对应交点为）大于，表明是左图的情况；如果小于等于 0，表明是右图的情况，这条光线是在介质内的折射光线。

使用球体表示场景

代码定义了一个 spheres 数组来表达整个场景，每一个球体分别是：

左侧墙体，红色；墙体的半径都很大，观者感知不到曲率；墙体的反射类型都是散射，但是颜色有所不同。
右侧墙体，蓝色。
后面墙体，灰色。
前面墙体，黑色。
底部墙体，灰色。
顶部墙体，灰色。
左侧球体，镜面材质。
右侧球体，透明玻璃材质，光线可能折射进入玻璃中继续传播。
顶部的光源，发射出强度为 12 的白光。

Sphere spheres[] = { //Scene: radius, position, emission, color, material
  Sphere(1e5, Vec( 1e5+1,40.8,81.6), Vec(),Vec(.75,.25,.25),DIFF),//Left
  Sphere(1e5, Vec(-1e5+99,40.8,81.6),Vec(),Vec(.25,.25,.75),DIFF),//Rght
  Sphere(1e5, Vec(50,40.8, 1e5),     Vec(),Vec(.75,.75,.75),DIFF),//Back
  Sphere(1e5, Vec(50,40.8,-1e5+170), Vec(),Vec(),           DIFF),//Frnt
  Sphere(1e5, Vec(50, 1e5, 81.6),    Vec(),Vec(.75,.75,.75),DIFF),//Botm
  Sphere(1e5, Vec(50,-1e5+81.6,81.6),Vec(),Vec(.75,.75,.75),DIFF),//Top
  Sphere(16.5,Vec(27,16.5,47),       Vec(),Vec(1,1,1)*.999, SPEC),//Mirr
  Sphere(16.5,Vec(73,16.5,78),       Vec(),Vec(1,1,1)*.999, REFR),//Glas
  Sphere(600, Vec(50,681.6-.27,81.6),Vec(12,12,12),  Vec(), DIFF) //Lite
};

可以看出，坐标轴的原点位于盒子的左面、后面和底面的交点附近。宽度 100 左右，高度 80 左右，深度 170 左右。

准备渲染

在真正开始渲染之前，还需要做一些准备工作。

确定相机和输出图像

先跳过 clamp，toInt，radiance 这几个函数，直接来看 main 函数。

int main(int argc, char *argv[]){
  int w=1024, h=768, samps = argc==2 ? atoi(argv[1])/4 : 30;
  Ray cam(Vec(50,52,295.6), Vec(0,-0.042612,-1).norm()); // cam pos, dir
  Vec cx=Vec(w*.5135/h), cy=(cx%cam.d).norm()*.5135, r, *c=new Vec[w*h];
  for (int y=0; y<h; y++){                       // Loop over image rows
    fprintf(stderr,"\rRendering (%d spp) %5.2f%%",samps*4,100.*y/(h-1));
    for (unsigned short x=0, Xi[3]={0,0,(unsigned short)(y*y*y)}; x<w; x++)
      // ... 暂时先省略
  }
  FILE *f = fopen("image.ppm", "w");         // Write image to PPM file.
  fprintf(f, "P3\n%d %d\n%d\n", w, h, 255);
  for (int i=0; i<w*h; i++)
    fprintf(f,"%d %d %d ", toInt(c[i].x), toInt(c[i].y), toInt(c[i].z));
}

首先，定义需要渲染图像的宽度（1024），高度（768），对每个像素的采样次数（命令行参数传入，或 120 次）。注意，变量 samps 的值是采样次数的 1/4，在这个例子中，最终渲染在图像上的每一个像素，又会拆分成 4 个子像素进行追踪和采样，而 samps 的值是子像素的采样次数。

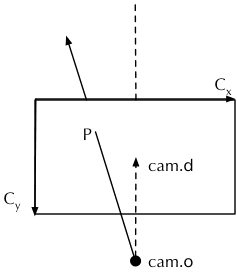
然后，使用射线类的变量 cam 来表示相机，射线的原点 cam.o 即是相机的位置，而射线的方向 cam.d 是相机朝向的方向。由于相机本身的位置只是一个点，所以需要把渲染出的图像视为在屏幕前方（亦或是后方，参考一下眼球和相机的构造）不远处的一块矩形幕布，抵达相机的光线穿透幕布时会在与幕布的交点处留下颜色，这样就在幕布上投影了。只要幕布的分辨率和宽高比不变，其距离相机的远近与最终结果是无关的，所以程序直接设定幕布与相机的距离是 1，设定幕布本身的高度为 0.5135（配合像素尺寸的宽高比，其实这里已经暗含了相机的水平和垂直视场角的信息）。然后，求取长度等于幕布真实宽度 0.5135*w/h 的水平矢量 cx（平行于 X 轴），求取长度等于幕布真实高度 0.5135 的垂直矢量 cy（通过 cx 与 cam.d 叉乘而来）。

再接着，生成长度为 w*h 的 Vec 类型数组 c 备用。这个数组的作用是存储渲染的结果。

最后，遍历宽度和高度，对每一个像素进行渲染，并将渲染得到值写入到数组 c 中，并将其输出为 PPM 格式的图片，以便打开查看渲染效果。

PPM 是一种基于文本的图片格式，能够帮助你避免考虑图片文件编码问题，轻易地按像素输出图片。比如以下文本内容就是一张 4x4 的图片。
P3
# feep.ppm
4 4
15
 0  0  0    0  0  0    0  0  0   15  0 15
 0  0  0    0 15  7    0  0  0    0  0  0
 0  0  0    0  0  0    0 15  7    0  0  0
15  0 15    0  0  0    0  0  0    0  0  0

总结一下各个变量的含义：

w 和 h：宽度和高度像素数。
samps：每个像素采样次数的 1/4。
cam：相机描述。
cx 和 cy：长度与幕布真实尺寸相同的水平、垂直矢量。
c：按像素存储渲染结果的数组。

子像素采样

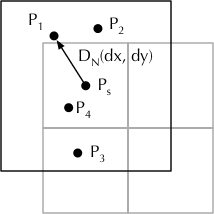
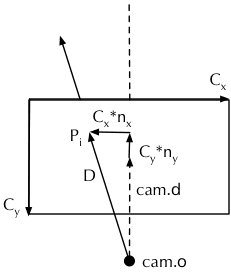
接下来，我们看一下如何计算每个像素的值的（即之前省略的部分）。对每一个像素，都将其拆分为 2x2 一共 4 个子像素。一个当然的想法是，以子像素的中心点作为射线的出发点开始追踪，但是由于每个子像素都会进行 samps 次光追取均值，所以这里就引入了一次随机过程：以子像素的中心点，在一个像素大小的范围内进行一次随机采样，并以采样到的点为射线的出发点，进行一次光追。对每个子像素完成 samps 次光追，依次以， ……为出发点，最后求均值。

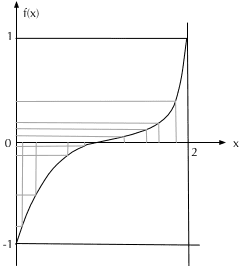
而且，为了使渲染的质量更高一些（达到相同渲染质量所需的采样次数更小一些），这里对随机过程进行了优化：对随机数进行了一次 tent 滤波。此滤波函数将从区间映射到了，当为随机的值时，的分布更向中点值集中（从图中可以看出）。

然后，拿到经过滤波后的随机数，，计算在整个画布中的归一化坐标（假设成为和，如 nx=(sx+0.5+dx)/2+x)/w-0.5），再乘以之前求得的画布真实尺寸矢量和，加上相机本身的方向矢量，就得到了最终从相机原点射向的矢量，即代码中的 d。

for (int sy=0, i=(h-y-1)*w+x; sy<2; sy++)     // 2x2 subpixel rows
    for (int sx=0; sx<2; sx++, r=Vec()){        // 2x2 subpixel cols
        for (int s=0; s<samps; s++){
            double r1=2*erand48(Xi), dx=r1<1 ? sqrt(r1)-1: 1-sqrt(2-r1);
            double r2=2*erand48(Xi), dy=r2<1 ? sqrt(r2)-1: 1-sqrt(2-r2);
            Vec d = cx*( ( (sx+.5 + dx)/2 + x)/w - .5) +
            cy*( ( (sy+.5 + dy)/2 + y)/h - .5) + cam.d;
            r = r + radiance(Ray(cam.o+d*140,d.norm()),0,Xi)*(1./samps);
        } // Camera rays are pushed ^^^^^ forward to start in interior
        c[i] = c[i] + Vec(clamp(r.x),clamp(r.y),clamp(r.z))*.25;
    }

最后，调用 radiance，沿着穿过此子像素的射线，在 140 倍远（让光追的开始点进到盒子里面，而不会直接被朝前的表面挡掉）的地方开始进行光线追踪算法。进行 samps 次，取均值，再基于 4 个子像素再取一次均值，就得到了这个像素的颜色。

erand48() 函数是 C 标准库提供的随机函数。传入长度为 3 的数组作为随机种子，返回 [0, 1] 区间的双精度浮点数，同时改写传入的随机种子，便于下一次调用 erand() 时传入（以获取一个不同的结果）。

总结一下各个变量的含义：

i：为当前像素在 c 中的索引。
r：通过光追计算出的子像素的颜色。
sx 和 sy：子像素索引，为 0 或 1。
r1 和 r2：滤波用自变量，在 [0, 2] 区间随机取得。
dx 和 dy：滤波后的随机自变量，分布在 [-1, 1] 区间内。
d ：从相机原点指向子像素位置的矢量。

光线追踪

讲了这么多，终于到正餐了。函数 radiance() 即进行了一次光线追踪。

Vec radiance(const Ray &r, int depth, unsigned short *Xi){
    double t;                               // distance to intersection
    int id=0;                               // id of intersected object
    if (!intersect(r, t, id)) return Vec(); // if miss, return black
    const Sphere &obj = spheres[id];        // the hit object
    Vec x=r.o+r.d*t, n=(x-obj.p).norm(), nl=n.dot(r.d)<0?n:n*-1, f=obj.c;
    double p = f.x>f.y && f.x>f.z ? f.x : f.y>f.z ? f.y : f.z; // max refl
    if (++depth>5) if (erand48(Xi)<p) f=f*(1/p); else return obj.e; //R.R.
    if (obj.refl == DIFF){                  // Ideal DIFFUSE reflection
      // ...
    } else if (obj.refl == SPEC)            // Ideal SPECULAR reflection
      // ...
    // ...                                   // Ideal dielectric REFRACTION
}

函数 radiance() 接收三个参数，射线 r，深度 depth 和随机种子 Xi。此函数是一个递归函数，在计算射线颜色时候，遇到反射或折射，会计算出下一次反射或折射的射线，然后递归调用自己求算下一次射线的颜色。深度 depth 标记了反射/折射的次数。

下面看 radiance() 函数的逻辑：

求取交点和递归结束条件

首先，对场景中的所有球体对象，尝试求取射线与之交点。函数 intersect() 负责做这件事：遍历 spheres 数组，依次调用 sphere 对象上的 intersect() 方法，并保留最小的正值 t 和对应球体在 spheres 数组中的索引 i。

inline bool intersect(const Ray &r, double &t, int &id){
    double n=sizeof(spheres) /sizeof(Sphere), d, inf=t=1e20;
    for(int i=int(n);i--;) if((d=spheres[i].intersect(r))&&d<t){t=d;id=i;}
    return t<inf;
}

如果没有任何对象与之相交，直接返回黑色（递归的结束条件 1）。

如果检测到有球体与射线相交，首先检查当前深度是否大于了 5（之前已经经过了 5 次反射或折射），如果是，那么遵循一个概率来随机地决定采取以下哪一种方案：

放弃反射光的贡献，直接返回物体的出射光——虽然大部分时候是 0（递归的结束条件 2）。
继续追踪光线。

这个概率就是当前物体表面的颜色 RGB 分量中最大的那个分量，归一化后的值。换言之，物体越暗（的颜色值越低），越容易被筛选到第 1 种方案（因为物体暗，环境光反射贡献的值也会小），而物体越亮，越容易被筛选到第二种方案。值得注意的是，当选择第二种方案时，需要把物体的颜色按照概率调高一些 f=f*(1/p)，这是因为那些运气不够好，被筛选到 1 方案光线，其反射分量完全地消失了，这会导致最终计算出的颜色的期望（也就是说，即使采样无穷次）与真实值产生偏差。在运气好的 2 方案中调整颜色，可以消除这个偏差。

按照概率进行随机选择是无处不在的，只要采样的次数足够多，那么遵照概率选择计算得到的均值就能够逼近真实值。

接着，如果深度小于等于 5，那么不管物体的颜色值如何，都会正常地递归地进行光线追踪。在此之前，还需要预先求取一些变量的值，比如法线 nl 等，便于后续使用。

总结一下各变量的意义：

t：交点距离相机原点的距离。
id：相交的球体在 spheres 数组中的索引。
obj：相交的球体 Sphere 对象。
x：交点的位置。
n：球体在交点处的归一化的法线（从球心射向表面）。
nl：与反射/折射上下文契合的归一化的法线：如果射线在球体外部，nl 与 n 相同；如果射线在球体内部（折射），nl 与 n 相反。

散射（漫反射）

追踪光线，当代表光线的射线与球体相交时，根据球体表面的特性，进行不同的操作（代码中省略的部分）。

如果物体表面是漫反射，将随机选取一个角度取归一化的反射光线：

确定互相正交的三个归一化矢量，和，其中为反射面的法线。
在区间中随机确定一个值，并使作为反射光线在法线方向上投影的长度，使也就是成为反射光线在表面上投影的长度。
在区间中随机确定一个角度值，使之成为反射光点在反射表面（即平面）的投影与轴的交角。
极坐标公式转笛卡尔坐标，计算出在半球面的随机矢量，再归一化得到反射矢量。

最后，递归地调用 radiance() 函数，将反射光线作为参数传入，传入已自增过一次的深度和随机种子。其结果乘以表面的颜色，再加上球体表面的发射光颜色，作为结果返回。这就是此光追算法对散射表面的处理。

if (obj.refl == DIFF){                  // Ideal DIFFUSE reflection
    double r1=2*M_PI*erand48(Xi), r2=erand48(Xi), r2s=sqrt(r2);
    Vec w=nl, u=((fabs(w.x)>.1?Vec(0,1):Vec(1))%w).norm(), v=w%u;
    Vec d = (u*cos(r1)*r2s + v*sin(r1)*r2s + w*sqrt(1-r2)).norm();
    return obj.e + f.mult(radiance(Ray(x,d),depth,Xi));

总结一下各变量的含义：

u，v，w：互相正交的三个归一化矢量，w 即为法向量。
r1：反射光线在反射表面与 u 的交角。
r2 与 r2s：r2s 为反射光线在反射表面投影的长度，r2 为此值的平方。
d：随机求取的反射方向。

镜面反射

镜面反射比较简单，因为对于确定的入射光线，反射的方向也是确定的，因此没有随机过程，直接取镜面反射的方向继续进行光追。

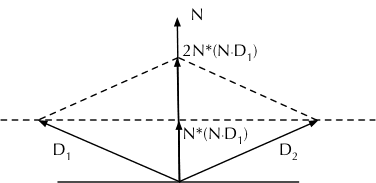
镜面反射的求法比较简单，不过也记录一下吧：如下图对称的两条射线和，而法线为（法线是归一化的）。此时有，求解。在代码中，就是 -r.d，带入得到 r.d-n*2*n.dot(r.d)，即反射光线的。由于 r.d 也已经是归一化的了，所以求取得到的结果也一定是归一化的。

代码如下：

} else if (obj.refl == SPEC)            // Ideal SPECULAR reflection
    return obj.e + f.mult(radiance(Ray(x,r.d-n*2*n.dot(r.d)),depth,Xi));

折射

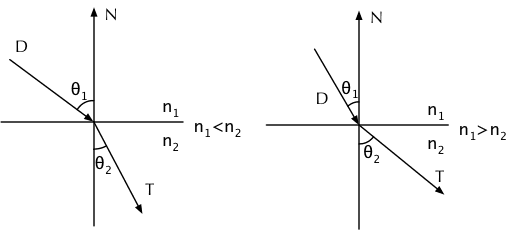
折射是比较复杂的。不同的物体有不同的折射率，空气的折射率为 1，玻璃的折射率为 1.5。根据折射定理：光线从折射率为的介质折射到折射率为的介质，折射角满足（此定理可以从更一般的麦克斯韦电磁方程组推导出来，厉害厉害）：

全反射

首先需要考虑的是全反射现象，即光线从光密介质（玻璃）向光疏介质（空气）传播时（上图右半部分），大于临界角（使得为 90° 的），以至于不存在满足上述折射定理时，所有光都被反射的现象，即：

两边平方并作简单变换，得到：

由于 nnt 为，而 ddn 为，代入上式，得到全反射的条件即是 1-nnt*nnt*(1-ddn*ddn))<0。满足全反射条件时，镜面反射的方式进行处理。

Ray reflRay(x, r.d-n*2*n.dot(r.d));     // Ideal dielectric REFRACTION
bool into = n.dot(nl)>0;                // Ray from outside going in?
double nc=1, nt=1.5, nnt=into?nc/nt:nt/nc, ddn=r.d.dot(nl), cos2t;
if ((cos2t=1-nnt*nnt*(1-ddn*ddn))<0)    // Total internal reflection
    return obj.e + f.mult(radiance(reflRay,depth,Xi));

总结一下各变量的含义：

reflRay：镜面反射方向，与上一节中的求法完全一致。
into：由空气（试图）进入玻璃则为 true，由玻璃（试图）进入空气则为 false。
nc 和 nt：空气和玻璃的折射率。
nnt 为折射率比值，当追踪的射线是从空气进入玻璃时，nnt 为 1.0/1.5，当射线是从玻璃进入空气时，nnt 为 1.5。
ddn：即的值，由和点乘而来。

正常折射

所谓正常折射，即是光线一部分镜面反射，一部分折射进入另一种介质。此时，我们需要：

计算折射光线矢量。
计算有多少比例的光线被反射，有多少比例的光线被折射。
根据条件，选择以随机或非随机的形式，递归地进行光线追踪。

首先计算折射光线矢量：

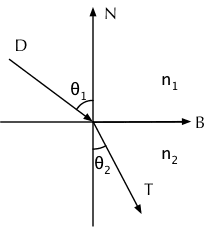
首先，假设入射光线在表面平面的投影矢量（并归一化）为已知，折射角也已知，我们可以得到为：

其中就是入射光线平面上的投影矢量（因为入射和折射在同一个平面内）归一化得到，而此投影矢量可以使用减去在法线上的投影（注意这里点积是个负数）来得出，因此：

同时的正弦和余弦值也可以通过折射定律求得：

全部代入，可得：

按照上述公式，将变量代入，即可计算出折射光线归一化矢量 tdir：

Vec tdir = (r.d*nnt - n*((into?1:-1)*(ddn*nnt+sqrt(cos2t)))).norm();

接下来，计算有多少比例的光线被反射，有多少比例的光线被折射。根据电动力学的一些理论，入射光线（普通的非偏振光）被反射/折射的比例，与入射角，两种介质的折射率都有关系。当入射角等于 0（即垂直入射到表面）时，被反射的比例为：

而当入射角为时的反射比例为：

最后，基于当前光追的深度：

如果深度小于等于 2，那么分别递归地追踪反射光和折射光，将两者对颜色的贡献再加上物体本身的发光，作为结果返回。
如果深度大于 2，那么依据折射和反射光线的占比来进行概率随机，选择追踪反射光或折射光中的一支。换言之，如果反射光占比高，那么就有较大的可能性随机到反射光线，反之亦然。注意，这时由于我们放弃了另一种可能性，会导致结果的期望产生偏差，所以需要进行一次修正。

对玻璃材质，前几次反射、折射对最终的结果的贡献比较大，所以选择都进行追踪。但是这样做一下子使得某些追踪的采样次数发散为了原来的 4 倍，如果深度改为 4，可能就是 16 倍。所以代码把发散深度限制在 2 这样一个比较小的数值，也算是在效果和性能间达到一个平衡。